User Defined Types

Aggregate Types

Sometimes you need to store multiple pieces of data in a single variable. Extempore has four types for this:

• Arrays
• Vectors
• Tuples
• Abstract Data Types

Arrays

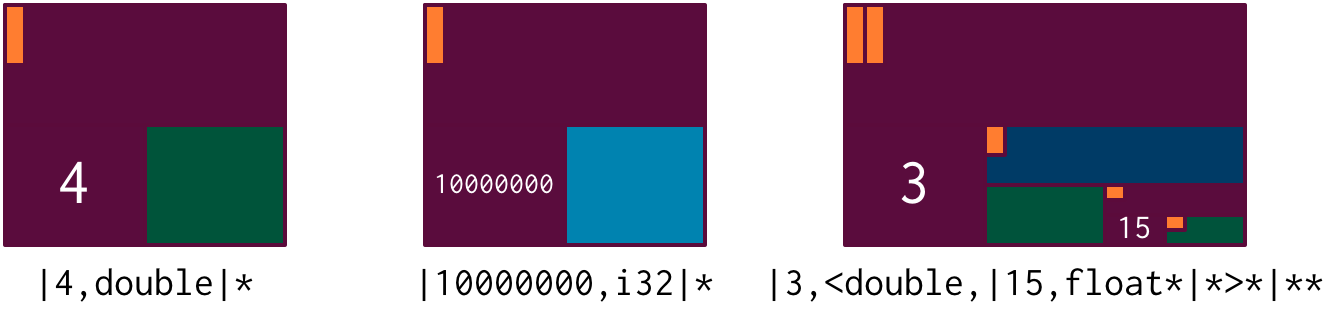
An array in xtlang is a fixed length array of elements of a single type (like a static C array). The array type signature specifies the length of the array, the type of the array elements, and is closed off with the pipe (|) character. For Example:

• |4,double|*: a pointer to an array of 4 double
• |10000000,i32|*: a pointer to an array of one million i32
• |3,<double,|15,float*|*>*|**: a pointer to a pointer to an array of pointers to 2-tuples, the second element of which is a pointer to an array of 15 float pointers. Whew!

Notice that all of these are pointers to arrays. When passing arrays around in Extempore we will always be passing a pointer to the array, rather than the array itself.

If we need to access the values in an array we can use aref. aref takes two arguments:

1. A pointer to the array
2. An integer index into the array (of type i64) where the index starts at 0.

If you try to reference an element that lies outside the array then the compiler will complain and your code won’t compile.

So for example given the array a:|4,double|* we can access it in serial order like this:

• (aref a 0)
• (aref a 1)
• (aref a 2)
• (aref a 3)

or use it in a function like this:

(bind-func get-member2
  (lambda (v:|4,i64|*)
    (aref v 2)))

But (aref a 4) won’t compile as a only has 4 elements.

You can also get the memory location of a member array using aref-ptr:

(bind-func get-member2:[i64*,|4,i64|*]*
  (lambda (v:|4,i64|*)
    (aref-ptr v 2)))

We can set values using aset!. aset! takes three arguments:

1. A pointer to the array.
2. An integer index into the array (of type i64) where the index starts at 0.
3. The new value for that index.

So for example given the array a:|4,double|* we can set each value to 0 like this:

• (aset! a 0 0)
• (aset! a 1 0)
• (aset! a 2 0)
• (aset! a 3 0)

and we can use it in a function like this:

;; Set every member of the array to 0
(bind-func zero-set
  (lambda (v:|4,i64|*)
    (let ((i 0))
      (dotimes (i 4)
        (aset! v i 0)))))

We could also do the same thing more succinctly using afill!:

• (afill! a 0 0 0 0) ;; set each value to 0
• (afill! a 1 2 3 4) ;; Set a[0] = 1, a[1] = 2, a[2] = 3, a[3] = 4

and redefining the function above we get this:

;; Set every member of the array to 0
(bind-func zero-set
  (lambda (v:|4,i64|*)
    (afill! v 0 0 0 0)))

You can also initialize arrays directly using array_ref:

;; Initialize and create an array
(bind-func test-array
  (lambda ()
    (let ((arr:|4,i64|* (array_ref 1 2 3 4)))
      (zero-set arr))))  ;; TODO should probably change this to print out to cmd line.

Vectors

A second aggregate data type in XTLang is the vector type. These are almost identical to arrays, but operations on vector types use the CPUs CIMD registers and instructions (assuming your hardware has them). For certain types of processing this can result in significant performance speedups, but Vectors are less flexible than arrays as they do not support conditionals and branching.

• /4,float/* - a pointer to a vector of four floats
• /256,i32/* - a pointer to a vector of 256 ints

The functions for working with vectors are also very familiar: vfill!, vset! and vref

Unless you know that the particular code you’re working on is the performance bottleneck in your system, it’s probably best to start out with arrays, and to change to vectors later on if it becomes necessary.

Tuples

A tuple is a fixed-length type also, but the elements of a tuple can be different types. The syntax for declaring a tuple in xtlang is <>. Like arrays and vectors, a tuple is always a pointer type:

• <double,i32>* - a pointer to a 2-tuple: the first element is a double and the second element is an i32
• <i64*,i64,float**>* - a pointer to a 3 tuple: the first element is a pointer to an i64, the second is an i64, and the third is a pointer to a pointer to a float
• <double,[i32,i32]*> - a pointer to a 2 tupe: the first element is a double, the second element is a closure of type [i32,i32]*.
• <i32,|4,i32|*> - a pointer to a 2 tupe: the first element is an i32, the second element is a an array of 4 i32s.

The functions for working with tuples are: tref, tset! and tfill!. These work identically to the functions aref, aset! and afill!. So given the tuple tup:<double,float,i64>*

• (tref tup 0) - will return the double value.
• (tset! tup 1 3.2) - will set the float value of tup to 3.2
• (tfill! tup 3.2 5.6 5) - will set the first element to 3.2:double, the second element to 5.6:float, the third element to 5:i64.

And finally, if you want a reference to (rather than the value of) an element in the tuple, use tref-ptr instead of tref:

• (tref-ptr tup 1) - will give you the memory location of the float value.

Custom Types

To round it off, you can also define your own types. This is convenient: it’s easier to type my_type than [double*,<i64,i32>,float,float], especially if it’s a type that you’ll be using a lot in your code.

There are two ways to define a custom type: bind-type and bind-alias.

Examples:

(bind-alias my_type_1 <i64,double>)
(bind-type my_type_2 <float,[i64,i32]*,|3,double|*>)

bind-type tells the xtlang compiler about your new type, which provides some safety benefits: the more the compiler knows about the types in your code, the more errors it can throw at compile time and save messy runtime errors and tricky debugging.

As an example, let’s make a 2D ‘point’ type, and a function for calculating the euclidean distance between two points.

(bind-type point <double,double>)

(bind-func euclid_distance
  (lambda (a:point* b:point*)
    (sqrt (+ (pow (- (tref a 0)
                   (tref b 0))
                2.0)
             (pow (- (tref a 1)
                     (tref b 1))
                  2.0)))))

To test this out, we can check the diagonal length of the unit square, which should be sqrt(2) = 1.41

(bind-func test_unit_square_diagonal
  (lambda ()
    (let ((bot_left:point* (alloc))
          (top_right:point* (alloc)))
      (tfill! bot_left 0.0 0.0)
      (tfill! top_right 1.0 1.0)
      (printf "The length of the unit square's diagonal is %f\n"
              (euclid_distance bot_left
                               top_right)))))

(test_unit_square_diagonal)

;; prints "The length of the unit square's diagonal is 1.414214"

Now, what happens if we change this testing example to make top_right and bot_left just plain tuples of type <double,double> instead of being our new point type.

(bind-func test_unit_square_diagonal_2
  (lambda ()
    (let ((bot_left:<double,double>* (alloc))
          (top_right:<double,double>* (alloc)))
      (tfill! bot_left 0.0 0.0)
      (tfill! top_right 1.0 1.0)
      (printf "The length of the unit square's diagonal is %f\n"
              (euclid_distance bot_left
                               top_right)))))

Now, instead of compiling nicely, we get the compiler error:

Compiler Error: Type Error: (euclid_distance bot_left top_right)
 function argument does not match. Expected "%point*" but got "{double,double}*"

Even though point is just a <double,double> (check the bind-type definition above), the compiler won’t let us compile the function. This is a good thing most of the time, because it makes us be more explicit about what we actually mean in our code, and saves us from the silly mistakes that can happen when we’re not clear about what we want.

There are lots of possibilities for the use of custom types, and there’s no problem with binding as many as you need to make your code and intention clearer. Binding custom types could, for instance, allow for the construction of a ‘data structures’ library like the C++ STL containers library or the Java collections framework.

bind-alias, in contrast to bind-type, is just a simple alias for the given type. The xtlang compiler, when it sees my_alias in the code, will simply substitute in the appropriate type (in this case <i64,|3,double|*>*) before it generates the LLVM IR to send to the compiler. bind-alias doesn’t tell the compiler as much about the code as bind-type does, which can lead to execution-time problems which would otherwise have been caught by the compiler. So you should almost always use bind-type over bind-alias.

Algebraic Data Types (ADTs)

While Algebraic Data Types work, they are currently slow to compile and have bad error messages. This is something that is being worked on, but in the meantime be warned…

Imagine that you have a shape type that can either be a circle, or a square: In Extempore we could create a type for this as follows:

;; load the adt library
(sys:load "libs/base/adt.xtm")

(bind-type point <double,double>)

(bind-data Shape
           (Circle point double)
           (Rect point point))

Note that ADTs are not part of the core library so you have to load the ADT library first.

Now that we’ve defined this ADT what can we do with it. Lets create a simple function that returns a circle:

(bind-func make-shape:[Shape*,point,double]*
  (lambda (pos:point rad:double)
    (Circle pos rad)))

There are two things to note here:

1. We can create a circle by calling a function that has the same name as the Shape type that we want. This function takes as parameters the values associated with Circle (there is a similar function called Rect.
2. Although we created a Circle this value has the type: Shape. The only way that we can create a Shape is by calling the functions Circle, or Rect.

Now that we have a Shape type, how do we use it? Let’s create a function that prints a shape:

(bind-func print-shape
  (lambda (shape:Shape*)
    (Circle$ shape (pos rad)
             (println "x: %f, y: %f, Radius: %f" (tref pos 0) (tref pos 1) rad)
             (Rect$ shape (point1 point2)
                    (println "x1: %f, y1: %f\nx2: %f, y2: %f"
                             (tref point1 0) (tref point1 1)
                             (tref point2 0) (tref point2 1))
                    void))))

The important functions here are Circle$ and Rect$. So where did they come from? When you create a new ADT with bind-data the xtlang compiler creates a macro for each sub-type that allows you to access the data. The macro name is the name of the sub-type followed by the ‘$’ sign. So for the Shape type we have the macros: Circle$ and Rect$.

So let’s examine the Circle$ macro more closely. This takes four arguments:

1. A variable of type Shape.
2. Two variables inside brackets: pos and rad. These variables are the two member variables for the Rect sub-type in the same order that are declared in the bind-data declaration above.
3. pos has type point.
4. rad has type double.
5. A form of type [!a]*. Where !a just means that this function can return any type.
6. This form has the variables point and rad declared as part of its lexical scope.
7. A second form of type [!a]. Where !a means that this function must return the same type as the previous form. This form does not have access to the variables point and rad.

Let’s consider what happens when shape = (Circle (point 3.0 4.0) 2.0). pos is given the value (point 3.0 4.0) and rad is given the value 2.0. These values are set as part of the lexical scope of the first form which is then called. The second form is ignored.

Now let’s consider the other scenario when shape = (Rect (point 3.0 4.0) (point 4.0 5.0)). The second form is called, everything else is ignored.

So Circle$ and Rect$ give us a way to write code that can respond differently according to which of the sub-types are passed in, and to access their data. Note that when calling Circle$ we don’t have to handle the situation where Shape is a Rect, all we have to do is to provide a default for when Shape is not a circle. If we want to handle all the sub-types of Shape then we need to use Rect$ as our default in Circle$. And this is exactly what we did for print-shape above.

This concludes our tour of the different types available to us in xtlang. Don’t worry at this stage if you don’t understand everything. In later chapters we will build upon what we’ve discussed in this chapter and this will develop your intuition for how these work.

Conclusion

In this chapter we’ve given you a whirlwind tour of the different types available in xtlang and how they are used. In the next chapter we will look some more at user defined types and some of the ways in which you can use them. If you’re still a little fuzzy on some of this stuff, the next chapter should help with that.