Audio signal processing
In Extempore you can write dynamic, hot-swappable DSP code. There is a special
function in the environment called (funnily enough) dsp. This is as simple as
declaring an xtlang closure (with a specific type signature) to be the audio
output ‘sink’. The values returned by this function are sent directly to the
audio driver and output as sound through the computer speakers. Every audio
sample (that is, at a rate of 44100Hz) this function is called with a few
arguments:
(bind-func dsp
(lambda (in:SAMPLE time:i64 chan:i64 data:SAMPLE*)
(* .1 (sin (/ (* 2.0 3.1415 ;; 2pi(ish)
440.0 ;; frequency (Hz)
(i64tof (% time 44100))) ;; time mod samplerate
44100.0)))))
;; to let Extempore know that this function is the one
;; it should call to get the output audio samples
(dsp:set! dsp)
This dsp function takes as input:
in: the input audio sample, e.g. from the microphonetime: ani64representing the timechan: anotheri64which represents the channel index (0for L,1for R, etc.). Extempore can handle any number of channels.data: this is a pointer to aSAMPLEtype (which isfloatby default), and can be used to pass arbitrary data into thedspfunction.
By default, the type of SAMPLE is float, it’s just a type alias:
(bind-alias SAMPLE float)
but it can also be double (if SAMPLE was an alias to double).
In the example above, I’m ignoring all of these arguments except for the time
argument, which I’m using to generate a simple sinusoid at 440Hz. Note the use
of the convert function, which converts time (which is an i64) to whatever
type SAMPLE is. But the cool thing is that like all functions in Extempore,
this dsp function can be redefined on-the-fly, as long as the type signature
stays the same. So, if I change the dsp function to
(bind-func dsp
(lambda (in:SAMPLE time:i64 chan:i64 data:SAMPLE*)
(* (convert 0.1 SAMPLE) (random))))
then the output changes to white noise. This is the real power of xtlang (and Extempore)—everything’s dynamic and modifiable at runtime, but it’s also performant enough to do sample-level manipulation in the same language and environment. So instead of the ugens (unit generators, e.g. oscillators) being locked up in a different language to the control language, it’s all mixed in together.
Abstraction and higher-order functions
Let’s create some oscillators:
(bind-func osc_c
(lambda (phase)
(lambda (amp freq:SAMPLE)
(let ((incr (* 2.0 3.1415 (/ freq 44100.))))
(set! phase (% (+ phase incr) (* 2.0 3.1415)))
(* amp (sin phase))))))
This osc_c function doesn’t return a primitive (int/float) value.
Rather, it returns a (pointer to a) closure, which is our ‘oscillator’
and takes an amplitude and a phase argument. This idiom is a useful one,
and comes up so much in xtlang code that by convention we give any
closure which returns another closure a _c suffix.
The type message printed by the compiler when we evaluate osc_c is:
Compiled osc_c >>> [[float,float,float]*,float]*
See that the return type of the osc_c function is [float,float,float]*: a
pointer to a closure which takes two float arguments and returns a float.
This is our oscillator, and we can use our osc_c function to create as many
oscillators as we need:
(bind-func dsp
(let ((osc1 (osc_c 0.0))
(osc2 (osc_c 0.0)))
(lambda (in:float time:i64 channel:i64 data:float*)
(cond
;; play a 200Hz tone in the left ear
((= channel 0) (osc1 0.25 200.0))
;; play a 300Hz tone in the right ear
((= channel 1) (osc2 0.25 300.0))
(else 0.0)))))
The phase variable in each of our oscillator closures is how we maintain state
between calls to osc1 or osc2. Each time the closure is called, phase gets
incremented (see the definition of osc_c above), and because phase is bound
within a let that is local to the returned closure, each osc has its own
phase value, so the oscillators created by osc_c are independent. In the
case above, they are each called with different frequencies to produce sine
tones of different pitch for each ear. This is closures in action, and it’s an
example of how the ‘scheme-like’ aspect of xtlang can simplify the job of
maintaining state.
It doesn’t take much imagination to see that much cooler stuff can be done in
dsp than just playing two sine tones. AM synthesis, FM synthesis, granular and
wavetable synthesis, as well as sampling and sample manipulation—these are all
possible. It’s worth noting that there are heaps better/easier ways to achieve a
lot of this stuff in Extempore: named constants for samplerate & 2pi, syntactic
sugar, library support etc are provided in the standard library (especially in
libs/core/audio_dsp.xtm). Still, it’s useful to build things up from first
principles to show how it all works.
Beyond pure tones
Playing a single sine tone is boring. Now, instead of just using the one oscillator, let’s use a few of them to generate a whole bunch of sine tones of different frequencies:
(bind-func osc_c ; osc_c is the same as last time
(lambda (phase)
(lambda (amp freq)
(let ((inc:SAMPLE (* 3.141592 (* 2.0 (/ freq 44100.0)))))
(set! phase (+ phase inc))
(* amp (sin phase))))))
;; remember that the dsp closure is called for every sample
;; also, let's add a type signature to the closure just because
;; we can. DSP is short for [SAMPLE,SAMPLE,i64,i64,SAMPLE*]*
(bind-func dsp:DSP
(let ((osc1 (osc_c 0.0))
(osc2 (osc_c 0.0))
(osc3 (osc_c 0.0)))
(lambda (in time channel data)
(cond ((= channel 1)
(+ (osc1 0.5 220.0)
(osc2 0.5 350.0)))
((= channel 0)
(osc3 0.5 210.0))
(else 0.0)))))
See how the let ‘outside’ the lambda sets up the three oscillators, then the
lambda closes over them and so each time the oscillator is called increments
its phase value appropriately?
Any number of oscillators (think of them as unit generators) can be bound and added in this way—this allows us to do additive synthesis. Having to define and refer to each osc individually doesn’t scale up very well, though, so it would be great if we could create and initialise them programmatically. This brings us to a couple of new (compound) types: tuples, and arrays.
Tuples in xtlang
As a refresher, tuples in xtlang are heterogeneous groupings of any xtlang types (just like a C
struct). They’re still statically typed, either explicitly or with the types
inferred from the types of other variables and literals. Syntactically, tuples
use angle brackets (<>).
When programming in xtlang you don’t really ever deal with tuples directly—you deal with them by reference through pointers. There are no ‘literals’ for tuples either—you can’t just go
(bind-func tuple_maker
(lambda (a:i64)
(let ((tup:<i64,i64> <a,a>))
tup)))
;; Compiler Error: unbound symbol: <a,a>
Instead, this time in the let we get a pointer to a tuple through a
call to alloc.
(bind-func tuple_maker
(lambda (a:i64)
(let ((tup:<i64,i64>* (alloc)))
(tset! tup 0 a)
(tset! tup 1 a)
tup)))
memory goes into more detail about this stuff,
but for now the key point is that the call to alloc returns a
pointer to a tuple of the specified type.
Notice the tset! function, which takes three arguments: a pointer to a
tuple (in the case above, that’s tup), an i64 (0-based) index for
specifying which ‘slot’ in the tuple we’re setting, and finally the
value to set it to (which must be of the appropriate type, otherwise
you’ll get a type error).
This new version of tuple_maker compiles—hooray! The type signature
printed by the compiler is Compiled tuple_maker >>> [<i64,i64>*,i64]*
and the type of tuple_maker is a pointer (denoted by the *) to a
closure (denoted by the []) which takes one i64 argument and returns
a pointer to a tuple of two i64 values.
Just to check that everything’s working properly, let’s write a little
test function
(bind-func test
(lambda (a:i64)
(let ((tup (tuple_maker a)))
(printf "<%d,%d>\n"
(tref tup 0)
(tref tup 1))
tup)))
(test 4) ; prints <4,4> (as it should!)
Tuples come in handy in lots of places, for instance we can use them to
rewrite one of the dsp functions from earlier (the one with the three
oscs)
(bind-alias osc_t [SAMPLE,SAMPLE,SAMPLE]*)
(bind-func dsp:DSP
(let ((osc_tuple:<osc_t,osc_t,osc_t>* (alloc)))
(tfill! osc_tuple (osc_c 0.0) (osc_c 0.0) (osc_c 0.0))
(lambda (in time channel data)
(cond ((= channel 1)
(+ ((tref osc_tuple 0) 0.5 300.0)
((tref osc_tuple 1) 0.5 420.0)))
((= channel 0)
((tref osc_tuple 2) 0.5 600.0))
(else 0.0)))))
This time, instead of binding each osc to its own symbol (osc1, osc2
and osc3), we created osc_tuple, a (pointer to a) tuple, which held
all the oscs. We filled it with tfill!, which takes as a first
argument the pointer to the tuple, and then enough additional arguments
to fill out the tuple. Equivalently, we could have set each element in
the tuple manually with (tset! osc_tuple 0 (osc_c 0.0)) etc.
Also, the use of bind-alias is helpful here, because it allows us to
condense the verbose type of the closure oscs
([SAMPLE,SAMPLE,SAMPLE]*) down to the more manageable osc_t, handy
when we then need to type the osc_tuple with three of them.
There’s no reason why the types in the tuple have to be the same. Indeed, usually they won’t be—tuples allow us to define more complex data structures which are suitable for the task at hand.
Arrays in DSP code
If tuples are xtlang’s structs, then arrays are (funnily enough)
xtlang’s arrays. Unlike tuples, which can be composed of heterogeneous
xtlang types, arrays are homogeneous (like a C array). The elements of
the array can be tuples, closures, or any valid xtlang type.
Syntactically, arrays are marked by pipes (|). Again, we access and
manipulate arrays through pointers returned by calls to the various
memory allocation functions (e.g. alloc). Instead of tref and
tset! (which we used for tuples), we use aref and aset!.
So, to bring this discussion back to the practical art of noise-making,
let’s create a dsp function which makes use of arrays and tuples to do
some additive synthesis. We’ll make an array osc_array, and then two
more arrays (amp_array and freq_array) to keep track of the
amplitude and frequency values.
(bind-func dsp:DSP
(let ((osc_array:|30,[SAMPLE,SAMPLE,SAMPLE]*|* (alloc))
(amp_array:|30,SAMPLE|* (alloc))
(freq_array:|30,SAMPLE|* (alloc))
(i 0))
;; initialise the arrays
(dotimes (i 30)
(aset! osc_array i (osc_c 0.0))
(aset! amp_array i (+ 0.2 (* 0.2 (random))))
(aset! freq_array i (+ 110.0 (* 1000.0 (random)))))
;; this is the dsp closure
(lambda (in time chan data)
(cond ((= chan 0) ; left channel
(let ((suml 0.0))
(dotimes (i 15) ; sum over the first 15 oscs
(set! suml (+ suml ((aref osc_array i)
(aref amp_array i)
(aref freq_array i)))))
(/ suml 15.0))) ; normalise over all oscs
((= chan 1) ; right channel
(let ((sumr 0.0))
(dotimes (i 15 15) ; sum over the remaining 15 oscs
(set! sumr (+ sumr ((aref osc_array i)
(aref amp_array i)
(aref freq_array i)))))
(/ sumr 15.0)))
(else 0.0))))) ; any remaining channels
This code is a bit more complex than the previous examples. Initially,
pointers to the three arrays (for the oscs, the amps and the freqs) are
set up in the let, then a dotimes goes through and sets them up with
the relevant data. The amplitudes and frequencies are chosen at random
(within sensible ranges). After the arrays have all been initialised in
the dotimes, the dsp lambda sums the output from the oscillators
(the first 15 oscs for the left channel and the last 15 oscs for the
right channel). That’s why the second dotimes takes an extra value in
the parens, this is an initial value (which defaults to zero) for the
loop variable to be bound to.
Remember that everything can be JIT-compiled whenever you like, so each
time the dsp closure is re-evaluated new random values will go into
the amp and freq arrays, and the additive dsp function will make a
different sound which you’ll hear straight away.
Now, choosing these values at random doesn’t necessarily lead to the most musical results, so it’s a good idea to choose them in some sort of systematic way. In our last example, we’ll play only the even harmonics of a given base frequency (I’ve also simplified the output to one channel for clarity).
(bind-func dsp:DSP
(let ((osc_array:|30,[SAMPLE,SAMPLE,SAMPLE]*|* (alloc))
(amp_array:|30,SAMPLE|* (alloc))
(freq_array:|30,SAMPLE|* (alloc))
(base_freq 110.0)
(i 0))
;; initialise the arrays
(dotimes (i 30)
(aset! osc_array i (osc_c 0.0))
(aset! amp_array
i
(if (= (modulo i 2) 0)
0.3
0.0))
(aset! freq_array i (* (convert (+ i 1) SAMPLE) base_freq)))
(lambda (in time chan data)
(let ((sum 0.0))
(dotimes (i 30)
(set! sum (+ sum ((aref osc_array i)
(aref amp_array i)
(aref freq_array i)))))
(/ sum 30.0))))) ; normalise over all oscs
See how we’re using the same arrays as last time (for osc, amp and freq)
but instead of randomly picking frequencies and amplitudes, we’re
generating a harmonic series with a fundamental of 110Hz, and only
playing the even harmonics (check the equality test in the
initialisation of amp_array). For fun, change that equality test to an
inequality test (<>) and listen to the result!
Packaging noise into instruments
This is hopefully beginning to flesh out the practice of doing real-time DSP in Extempore. It might seem like reinventing the wheel, building all the oscillators from scratch, but there are xtlang libraries for all of this, so there’s no need to mess around with the low-level synthesis stuff if you don’t want to. But the point is that you can, and it’s all hot-swappable, and written in the same language and environment that you use even if you just want to trigger pre-made instruments. These examples show how to do things from first principles, but feel free to mess around at whatever level of abstraction tickles your creative fancy.
To finish, we’ll make a really basic saw_synth instrument. An
instrument in Extempore allows you to trigger ‘notes’ like a MIDI soft
synth. note-level-music goes into a lot more
detail about how Extempore’s instrument infrastructure works, so this is
more of a ‘quick and dirty’ example instrument just to get a feel for
things. All the instrument code is just regular xtlang, and this
instrument (and others) can be found in libs/core/instruments.xtm and
libs/external/instruments_ext.xtm.
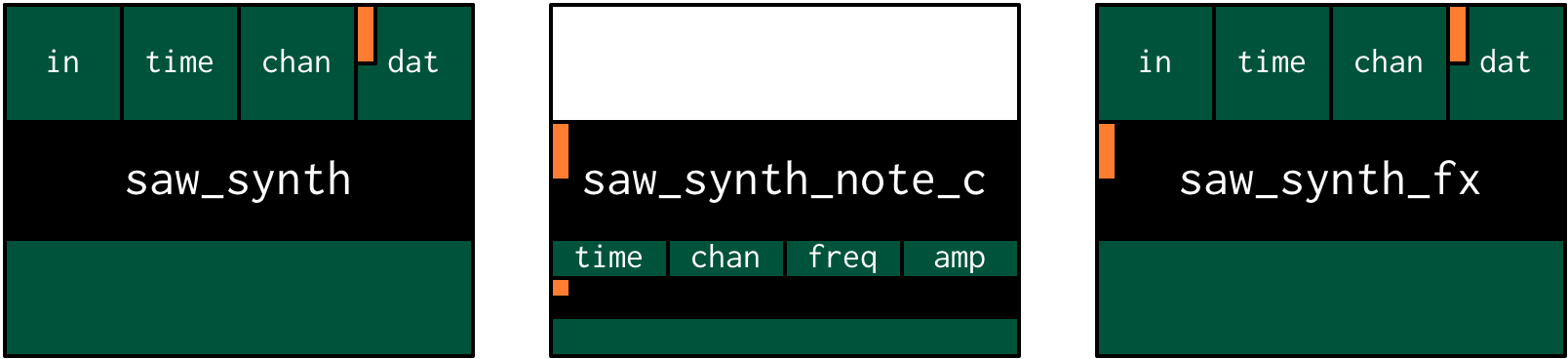
An instrument is basically two xtlang closures: a note kernel closure and an fx closure. These closures must have specific type signatures to play nice with the instrument signal chain.
Note kernel
First, let’s examine the note kernel closure. This closure takes zero arguments, and returns another closure which takes two arguments:
time: the current (sample) time in Extemporechan: the channel number
The returned closure will be called to provide the basic audio signal for the note, so that’s where we put our code to generate the saw wave.
(sys:load "libs/core/instruments.xtm")
(bind-func saw_synth_note
(lambda ()
(lambda (data:NoteData* nargs:i64 dargs:SAMPLE*)
(let (
;; the note is told when it was started; it needs this to figure out when to stop
;; notice that this is passed through the data argument with type NoteData*
(starttime (note_starttime data))
;; frequency is the pitch of the note as type SAMPLE
(frequency 440.0)
;; amplitude is the volume/loudness of the note as type SAMPLE
(amplitude 0.5)
;; SR = sample rate, so we want to play for 1 second, typically 44100 samples
(duration SR)
(saw (saw_c 0.)))
(lambda (time:i64 chan:i64)
;; when the notes has played for its duration, we disable it
(if (> (- time starttime) duration) (note_active data #f))
(if (= chan 0)
(saw amplitude frequency)
0.0))))))
;; when we evaluate saw_synth_note, the compiler prints:
;; Compiled: saw_synth_note >>> [[[float,i64,i64]*,NoteData*,i64,float*]*]*
Notice that the saw
unit-generator (ugen)
saw is bound (by calling saw_c) outside the inner lambda form.
This inner lambda defines the closure which will be returned by
saw_synth_note. In this returned closure, the ugen saw (which is
itself an xtlang closure) is called with the amplitude and frequency
values which are hard coded in the outer lambda form. The value
returned by the saw closure (as it is called repeatedly, once per
audio sample) will trace out a sawtooth
wave.
You might be wondering about the data:NoteData* argument that is
passed as the first argument to the note kernel closure. When a note is
played, this structure will contain information about the note: when the
note was started, what frequency the note should be played at, how loud,
and how long to play the note for. In this example we are only using it
to determine the start time because we need that to disable the note
when it is finished.
This is just a mono note kernel at this stage, because saw is only
called when chan is equal to 0. The note kernel closure will
actually be called once for each output channel, and the chan
argument will range from 0 for the first output channel to n - 1 for
the nth output channel (the number of output channels you have will
depend on your audio device). It’s therefore easy to generalise our note
kernel to multiple channels, so let’s make it a stereo note kernel
(bind-func saw_synth_note
(lambda ()
(lambda (data:NoteData* nargs:i64 dargs:SAMPLE*)
(let ((starttime (note_starttime data))
;; we're now pulling this information from data
(frequency (note_frequency data))
(amplitude (note_amplitude data))
(duration (note_duration data))
(sawl (saw_c 0.))
(sawr (saw_c 0.)))
(lambda (time:i64 chan:i64)
(if (> (- time starttime) duration) (note_active data #f))
(cond ((= chan 0) (sawl amplitude frequency))
((= chan 1) (sawr amplitude frequency))
(else 0.0)))))))
Now we make two saw ugens (sawl and sawr), and call the appropriate
one depending on the chan argument. Notice that we’re getting our note
information from the data argument instead of hard-coding it. Our
stereo saw note kernel is now ready to play!
Adding fx to the instrument
Often, you’ll want to add an audio effect to the instrument’s output—maybe a delay, a reverb, or some more outlandish audio processing. But we don’t want to apply the fx processing to each note individually, but rather to the total audio output of the instrument. And that’s where the fx closure comes in.
The most important argument to the fx closure is the in argument,
which represents the (dry) input signal that you want to process. It
is necessary to have an fx closure in your Extempore instrument,
although it may just pass its input through untouched:
(bind-func saw_synth_fx
(lambda ()
(let ((notekernel:NOTE_KERNEL null))
(lambda (in:SAMPLE time:i64 chan:i64 dat:SAMPLE*)
in))))
;; when we evaluate saw_synth_fx, the compiler prints:
;; Compiled saw_synth_fx >>> [i64,i64,i64,float,float*]*
Let’s add a stereo delay to make things a bit more interesting
(bind-func saw_synth_fx 200000 ; extra memory for the delay lines
(lambda ()
(let ((notekernel:NOTE_KERNEL null)
(delayl (delay_c 22050))
(delayr (delay_c 22050)))
(lambda (in:SAMPLE time:i64 chan:i64 dat:SAMPLE*)
(cond ((= chan 0)
(delayl in 0.3 0.2))
((= chan 1)
(delayr in 0.3 0.2))
(else 0.0))))))
Nice one. Also, remember that you change the fx closure at any time (just edit the code and re-evaluate it).
Putting it all together
Finally, to complete the instrument, we use a special make-instrument
macro
(make-instrument saw_synth saw_synth)
As long as your kernel (saw_synth_note) and fx (saw_synth_fx)
closures have the right signature, then evaluating the above line should
print for you
New instrument bound as saw_synth in both scheme and xtlang
and now the instrument is ready to play.
What—is that the end? Well, that’s a bit frustrating: we haven’t even
got to play our instrument yet! Don’t worry, we’ll use our saw_synth
instrument in note-level-music. Here’s a sneak
peek so you can hear it now though:
(bind-func dsp:DSP
(lambda (in time chan dat)
(if (< chan 2)
(saw_synth in time chan dat)
0.0)))
(dsp:set! dsp)
(play-note (now) saw_synth (random 60 90) 80 44100)
There are a couple of things to note which might be helpful for when you want to build your own instruments
- The note kernel closure (in this example
saw_synth_note) returns a closure for each note: multiple notes may be playing simultaneously (polyphony), so you want to make sure that each closure keeps track of the state it needs and doesn’t leak that state to any of the other notes which are playing simultaneously. - Each note kernel returns it’s output one sample at a time. So it’s up to you to make sure that these samples (when streamed to the audio hardware as an audio signal) make the audio waveform you’re after.
If you’re interested in a more in-depth explanation of Extempore’s instrument infrastructure, then you can go and build your own tonewheel organ <making-an-instrument>.